This article involves the way we measured the distance of Earth from the sun. This was done by taking advantage of the 3^rd law of Kepler. In order to do this we used the trajectories of Earth and Venus. Venus is the immediately inner planet towards the sun from the earth. The eccentricity of the orbit of earth is 0,017 and the eccentricity of the orbit of Venus is almost 0,007 (0,0067772). This means that both orbits can be considered almost circular. Let’s prove the 3^rd law of kepler for a circular orbit:

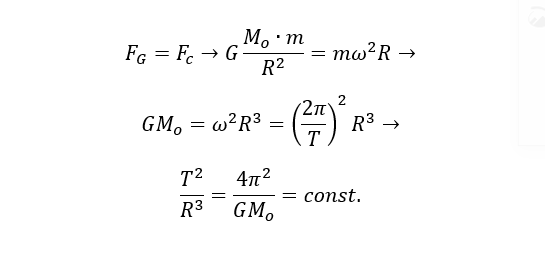
Where T is the period of the orbit of the planet, R is the distance from the star, M_o is the mass of the star and G the Gravitational constant.

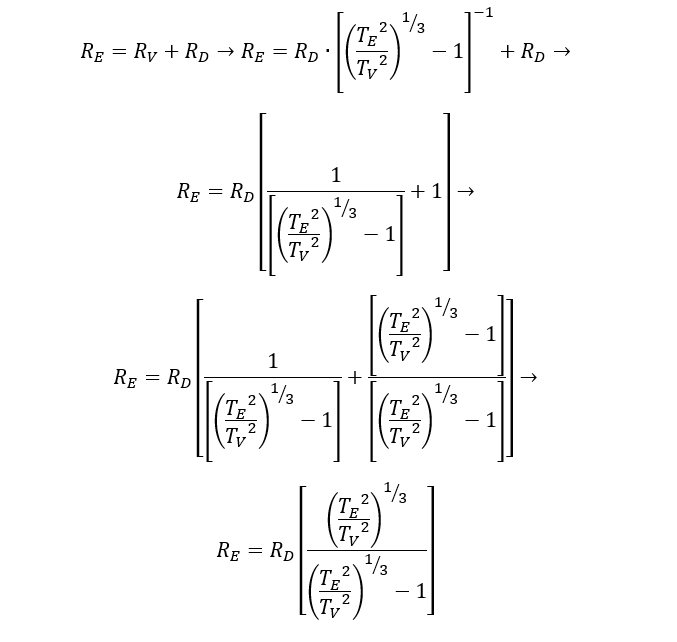
What we did to measure earth's distance from the sun was that we sent a laser beam to Venus and measured the time it took to bounce back to our planet. Thus since the beam of the laser travels with the speed of light (299.792.458m/sec), we measured the distance from Earth to Venus R_D and as a result the distance of Earth to the Sun R­­_E by taking advantage of the following calculation:

T_V: Period of orbit of Venus around Sun,     R_V: Distance between Venus and Sun

T_E: Period of orbit of Earth around Sun,       R_E: Distance between Earth and sun

Now to calculate the distance of earth to the sun we just added the distance to Venus R_D to the radius of the orbit of Venus R_V :